Aktien-Gewichtung in meinem Portfolio
Über die Aktiengewichtung in einem Portfolio aus ETFs und Einzelaktien
Klassische ETF-Anlage-Strategien legen Wert auf die Diversifizierung der Investionen und auf die Vermeidung von Überschneidungen, was bedeutet, dass eine einzelne Aktie idealerweise nur in einem der investierten ETFs indexiert ist.
Benchmarks wie ein S&P 500-Portfolio, das 60/40-Portfolio (60 % Aktien, 40 % Staatsanleihen) oder das 70/30-Portfolio (70 % MSCI World, 30 % MSCI EM) haben keine Überschneidungen und sind über Sektoren (S&P 500, 60/40, 70/30), Regionen (70/30) oder Anlageklassen (60/40) diversifiziert.
Portfolios mit verschiedenen ETFs, die eine bestimmte Schnittmenge bilden, sollen - diesen Strategien folgend - vermieden werden. So ist es nicht sinnvoll, sowohl einen S&P 500 als auch einen MSCI World zu besparen, da durch den hohen USA-Anteil im MSCI-World (über 60 %) die Schnittmenge zu groß ist.
Die Realität sieht jedoch oftmals anders aus. In vielen Fällen folgen Anleger nicht der reinen Lehre, sondern haben abgewandelte Portfolios. Die Portfolios enthalten beispielsweise Einzelaktien, die auch in ETFs enthalten sind, oder im Laufe der Jahre wurde die Anlagestrategie angepasst, so dass ETFs ausgewechselt wurden, ohne die zuvor besparten ETFs zu verkaufen.
So ist auch die Situation in meinem Portfolio. Meinem Alter und meiner Risikobereitschaft entsprechend ist es ein reines Aktienportfolio mit einem Schwerpunkt auf wachstumsorientierte Werte aus dem US-amerikanischen Technologiesektor. Die Einzelwerte sind teilweise sehr kleine Positionen, die zum Teil aus einer Laune heraus gekauft wurden. Bei den ETFs hat sich meine Strategie eher evolutionär weiterentwickelt.
Dass es größere Überschneidungen geben muss, war mir bewusst. Ich konnte jedoch nicht konkret beziffern, wie groß diese sind und auch nicht präzise quantifizieren, in welchem Ausmaß, einzelne Werte mein Portfolio dominieren.
Ich wollte jedoch gerne wissen, wie groß beispielsweise der Anteil an Apple-Aktien in meinem Gesamtportfolio ist. Ich habe zunächst nach einem Online-Tool gesucht, das mir erlaubt, meine einzelnen Investitionen einzugeben, um anschließend die Gewichtung angezeigt zu bekommen. Ein solches Tool habe ich jedoch noch nicht gefunden. Dabei ist es sicherlich für viele Anleger interessant, diese Informationen zu bekommen.
Mathematisch ist diese Aufgabe einfach zu lösen. Die einzelnen Aktien eines ETFs müssen entsprechend ihrer Gewichtung im ETF mit dem Anteil, den der ETF am Gesamtportfolio ausmacht, multipliziert werden. Dies muss für alle ETFs im Portfolio wiederholt werden.
Anschließend müssen die Ergebnisse der einzelnen Werte summiert werden. So kann ermittelt werden, welchen Anteil eine einzelne Aktie über alle Investitionen hinweg (ETFs und Einzelaktien) am Gesamtportfolio hat.
Im Folgenden werde ich die einzelnen Schritte der Datenextraktion, -transformation und -analyse transparent machen.
Gewichtung des Portfolios
Der erste Schritt ist eine Aufstellung meines Portfolios, das eine Gewichtung der einzelnen Positionen beinhaltet. Mein Depot (Stand 28.2.2021) sieht folgendermaßen aus:
## # A tibble: 11 x 3
## Name Kategorie Anteil_Proz
## <chr> <chr> <dbl>
## 1 NASDAQ 100 ETF 0.22
## 2 MSCI World ETF 0.165
## 3 MSCI Inf. Tech. ETF 0.035
## 4 Deutsche Telekom Einzelaktie 0.137
## 5 Apple Einzelaktie 0.112
## 6 Amazon Einzelaktie 0.094
## 7 Nvidia Einzelaktie 0.084
## 8 Square Einzelaktie 0.069
## 9 Deutsche Bank Einzelaktie 0.047
## 10 Twitter Einzelaktie 0.0259
## 11 Activision Einzelaktie 0.015Die Daten der ETFs
Für den zweiten Schritt habe ich die Daten der ETFs benötigt. Eine brauchbare Liste mit den gewichteten Bestandteilen der ETFs zu bekommen, hat sich als nicht ganz einfach herausgestellt. Es gibt zunächst keine Schnittstelle, über die die Bestandteile eines ETFs und seine Gewichtung abgefragt werden können. Auf den Webseiten der ETF-Anbieter sind jedoch teilweise HTML-Tabellen hinterlegt, die die nötigen Informationen enthalten. Viele dieser Daten haben sich jedoch als unbrauchbar herausgestellt, da sie nicht die International Securities Identification Number (ISIN) enthalten. Ohne diese Nummer lassen sich große ETFs mit hunderten Einzeltiteln nicht analysieren. Die Namen der Aktienunternehmen konnten nicht verwendet werden, da es zu viele verschiedene Schreibweisen gibt und selbst das Ticker-Symbol (AAPL oder AMZN) nicht eindeutig ist, da es sich doppeln kann wie das Beispiel DTE zeigt, das sowohl für Deutsche Telekom als auch für DTE Energy verwendet wird.
Brauchbare Daten mit ISIN habe ich auf den Seiten von iShares gefunden.
Laden der Daten
Die Daten wurden mit Copy-und-Paste von der Website in eine Excel-Tabelle übertragen und anschließend mit der Funktion read_excel in R eingelesen.
NASDAQ_100 <- read_excel("~/blog/Constituents_Weights_Indices.xlsx",
sheet = "NASDAQ 2", col_names = FALSE)
MSCI_World <- read_excel("~/blog/Constituents_Weights_Indices.xlsx",
sheet = "MSCI World 2", col_names = FALSE)
MSCI_Info <- read_excel("~/blog/Constituents_Weights_Indices.xlsx",
sheet = "MSCI Info 2", col_names = FALSE)Aufbereiten der Daten
Die Daten wurden mit Spaltennamen versehen und eine zusätzliche Spalte mit der Gewichtung im Gesamtportfolio (Gewichtung Einzelwert im ETF * Gewichtung ETF im Portfolio) hinzugefügt. Anschließend wurden nur die notwendigen Spalten mit dem Ticker-Symbol, der ISIN und der Portfolio-Gewichtung ausgewählt.
colnames(NASDAQ_100) <- c("Symbol", "Company", "Weight", "ISIN")
NASDAQ_100 <- NASDAQ_100 %>%
mutate(Weight = Weight / 100) %>%
mutate(Weight_Perc_Nasdaq_100 = Weight * 0.2195) %>%
select(1, 4, 5)Das Ergebnis war folgende Tabelle (als tibble):
print(NASDAQ_100)
## # A tibble: 102 x 3
## Symbol ISIN Weight_Perc_Nasdaq_100
## <chr> <chr> <dbl>
## 1 AAPL US0378331005 0.0246
## 2 MSFT US5949181045 0.0207
## 3 AMZN US0231351067 0.0184
## 4 TSLA US88160R1014 0.00957
## 5 GOOG US02079K1079 0.00801
## 6 FB US30303M1027 0.00733
## 7 GOOGL US02079K3059 0.00727
## 8 NVDA US67066G1040 0.00601
## 9 PYPL US70450Y1038 0.00542
## 10 INTC US4581401001 0.00450
## # … with 92 more rowsDiese Schritte habe ich für die zwei anderen ETFs in meinem Portfolio, den MSCI World und den MSCI Information Technology wiederholt.
Hier der MSCI World:
colnames(MSCI_World) <- c("Symbol", "Company", "Weight", "ISIN")
MSCI_World <- MSCI_World %>%
mutate(Weight = Weight / 100) %>%
mutate(Weight_Perc_MSCI_World = Weight * 0.1654) %>%
select(1, 4, 5)
head(MSCI_World)
## # A tibble: 6 x 3
## Symbol ISIN Weight_Perc_MSCI_World
## <chr> <chr> <dbl>
## 1 AAPL US0378331005 0.00647
## 2 MSFT US5949181045 0.00514
## 3 AMZN US0231351067 0.00407
## 4 FB US30303M1027 0.00192
## 5 GOOG US02079K1079 0.00190
## 6 GOOGL US02079K3059 0.00190Und hier der MSCI Information Technology:
colnames(MSCI_Info) <- c("Symbol", "Company", "Weight", "ISIN")
MSCI_Info <- MSCI_Info %>%
mutate(Weight = Weight / 100) %>%
mutate(Weight_Perc_MSCI_Info = Weight * 0.0352) %>%
select(1, 4, 5)
head(MSCI_Info)
## # A tibble: 6 x 3
## Symbol ISIN Weight_Perc_MSCI_Info
## <chr> <chr> <dbl>
## 1 AAPL US0378331005 0.00639
## 2 MSFT US5949181045 0.00508
## 3 V US92826C8394 0.00111
## 4 NVDA US67066G1040 0.00101
## 5 MA US57636Q1040 0.000979
## 6 PYPL US70450Y1038 0.000876Anschließend wurde die Tabelle mit den Einzelaktien erstellt.
ISIN <- c("DE0005557508", "US0378331005", "US0231351067", "US67066G1040", "US8522341036", "DE0005140008", "US90184L1026", "US00507V1098")
Symbol <- c("DTE", "AAPL", "AMZN", "NVDA", "SQ", "DBK", "TWTR", "ATVI")
Weight_Perc_Single_Stocks <- c(0.137, 0.112, 0.094, 0.084, 0.069, 0.047, 0.0259, 0.015)
Single_Stocks <- data.frame(Symbol, ISIN, Weight_Perc_Single_Stocks)
as_tibble(Single_Stocks)
## # A tibble: 8 x 3
## Symbol ISIN Weight_Perc_Single_Stocks
## <chr> <chr> <dbl>
## 1 DTE DE0005557508 0.137
## 2 AAPL US0378331005 0.112
## 3 AMZN US0231351067 0.094
## 4 NVDA US67066G1040 0.084
## 5 SQ US8522341036 0.069
## 6 DBK DE0005140008 0.047
## 7 TWTR US90184L1026 0.0259
## 8 ATVI US00507V1098 0.015Die verschiedenen Tabellen wurden mit der Funktion join_all zusammengefügt.
weight_all <- plyr::join_all(list(NASDAQ_100, MSCI_World, MSCI_Info, Single_Stocks), by = "ISIN", type = "full")Danach wurde die Summe der Werte aus Zahlenreihen der verschiedenen Tabellen gebildet und die Werte in absteigender Reihenfolge sortiert.
weight_all <- weight_all %>%
replace(is.na(.), 0) %>%
mutate(sum = rowSums(.[3:6])) %>%
arrange(desc(sum)) %>%
mutate(sum = sum * 100)
as_tibble(weight_all)
## # A tibble: 1,562 x 7
## Symbol ISIN Weight_Perc_Nas… Weight_Perc_MSC… Weight_Perc_MSC…
## <chr> <chr> <dbl> <dbl> <dbl>
## 1 AAPL US03… 0.0246 0.00647 0.00639
## 2 DTE DE00… 0 0.000198 0
## 3 AMZN US02… 0.0184 0.00407 0
## 4 NVDA US67… 0.00601 0.00103 0.00101
## 5 SQ US85… 0 0.000265 0.000260
## 6 DBK DE00… 0 0.0000827 0
## 7 MSFT US59… 0.0207 0.00514 0.00508
## 8 TWTR US90… 0 0.000165 0
## 9 ATVI US00… 0.00134 0.000232 0
## 10 TSLA US88… 0.00957 0.00159 0
## # … with 1,552 more rows, and 2 more variables:
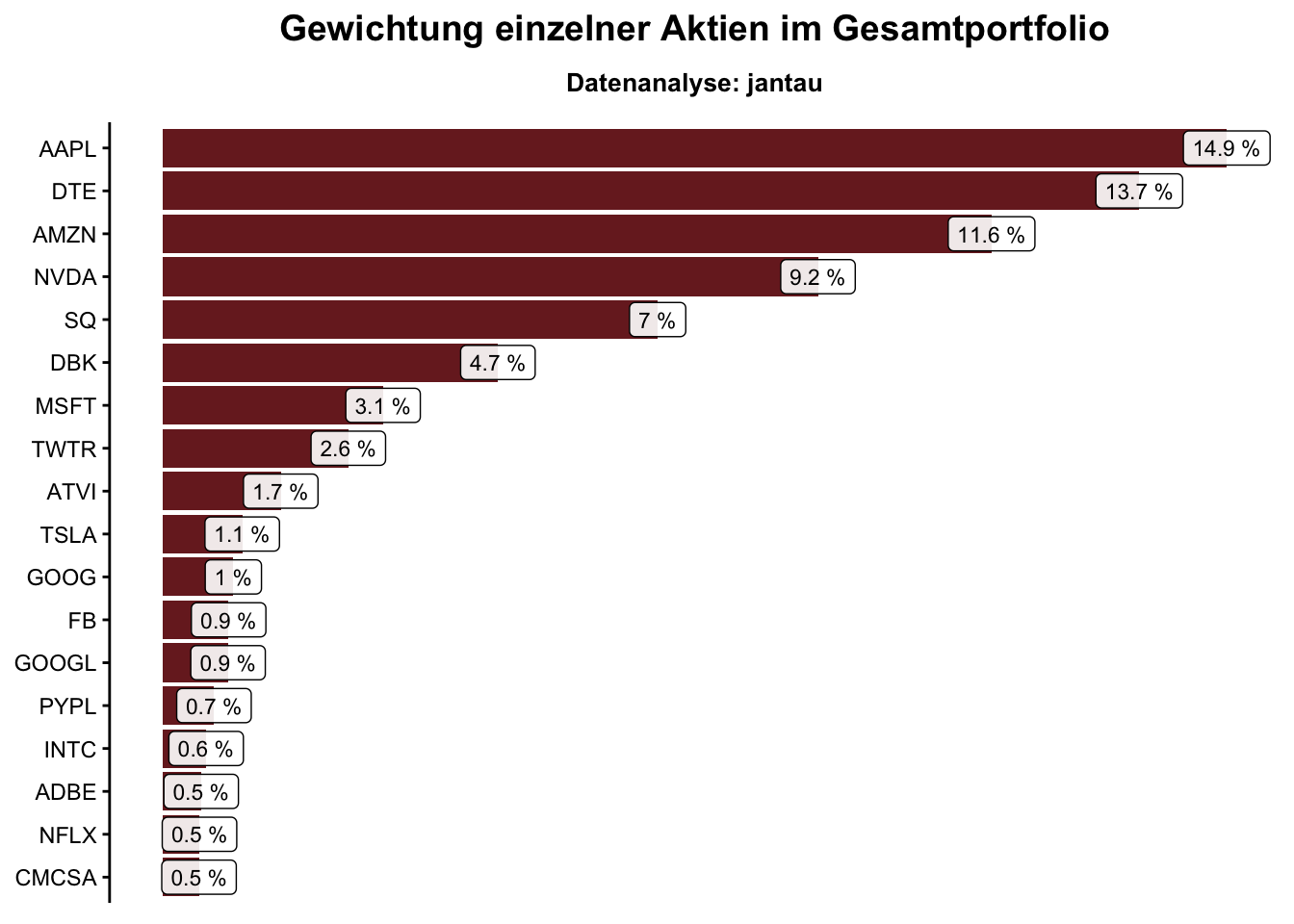
## # Weight_Perc_Single_Stocks <dbl>, sum <dbl>Zuletzt wurden die Ergebnisse mit einem ggplot-Barplot visualisiert. Hier habe ich mich auf die Werte konzentriert, die einen Anteil von 0,5 % oder mehr vom Gesamtportfolio ausmachen. Es handelt sich um 18 Werte.
pal <- got(1, option = "Daenerys", direction = 1)
weight_all %>%
filter(sum >= 0.5) %>%
ggplot(aes(x = reorder(Symbol, sum), y = sum)) +
geom_col(fill = pal) +
geom_label(
aes(label = paste0(round(sum, 1), " %")),
show.legend = FALSE,
size = 3,
alpha = 0.9
) +
coord_flip() +
theme_jantau +
labs(title = "Gewichtung einzelner Aktien im Gesamtportfolio",
subtitle = "Datenanalyse: jantau") +
theme(
axis.line.x = element_blank(),
axis.text.x = element_blank(),
axis.ticks.x = element_blank(),
axis.title.x = element_blank(),
axis.title.y = element_blank()
)
Ergebnis
Was sind die Ergebnisse dieser Analyse? Intuitiv hatte ich einen noch größeren Anteil der Schwergewichte erwartet, und zwar, dass die Apple-Aktien einen großen Anteil am Portfolio ausmachen. Intuitiv bin ich sogar von einem größeren Anteil als 14,9 % ausgegangen.
Einzelwerte haben einen erheblichen Einfluss auf die Zusammensetzung des Portfolios, was daran liegt, dass Einzelwerte zusammengenommen einen größeren Anteil am Portfolio haben, als die drei ETFs zusammen.
Die 18 größten Werte machen einen Anteil von 75 % im Portfolio aus. Die übrigen 1544 Werte machen zusammengenommmen die restlichen 25 % aus.
Zwei Aktien, die ich als Einzelaktien besitze, sind in allen drei von mir gehaltenen ETFs enthalten. Es handelt sich um Apple und um Nvidia.
Ich finde es durchaus aufschlussreich, eine Gewichtung des gesamten Portfolios nach Einzelwerten zu betrachten. Es ermöglicht mir, das Risiko des Portfolios besser beurteilen zu können und gegebenenfalls die Gewichtung nachzujustieren. Es wäre schön, wenn es ein Online-Tool gäbe, mit dem diese Untersuchtung einfach reproduziert werden könnte.
Den für diesen Beitrag erstellten Code findest du hier: https://github.com/jantau/jantau
Hat dir der Post gefallen? Melde dich für meinen Newsletter an, um über neue Beiträge informiert zu werden.