% Gewinn vs. % Verlust
Über den %-Gewinn, der benötigt wird, um einen %-Verlust auszugleichen
Eine Aktie verliert an einem Tag 1 % an Wert. Wie viel muss sie am nächsten Tag steigen, um den ursprünglichen Wert zu erreichen? Die intuitive Antwort “Um 1 %!” ist falsch. Die Aktie muss nicht um 1 %, sondern um 1,010101 % steigen, um den ursprünglichen Wert zu erreichen. Einfacher ist dieser mathematische Effekt zu begreifen, wenn sich der Wert der Aktie halbiert, also um 50 % fällt. Der Wert einer Aktie beträgt 100 Euro. Sie verliert 50 % ihres Werts, ist nunmehr nur noch 50 Euro wert. Sie muss 50 Euro zulegen, ihr Wert muss sich verdoppeln, also um 100 % steigen, um wieder zum Ausgangspunkt zu gelangen.
Die exponentielle Entwicklung ist rasant. Verliert eine Aktie 80 % ihres Wertes, so muss sie um 400 % steigen, um den Verlust wieder wett zu machen. Verliert die gleiche Aktie 81 %, so muss sie bereits 426.315789 % zulegen, um zum Ursprungswert zu gelangen. Eine Aktie, die 99 % verliert, muss 9900 % gewinnen. Und eine Aktie, die 100 % an Wert verloren hat? Ok, ich denke, ihr habt das Prinzip verstanden.
Die folgende Grafik zeigt die exponentielle Entwicklung. Auf der X-Achse ist der Verlust in Prozent angezeigt. Die Y-Achse zeigt, wie hoch der Gewinn sein muss, um den auf der X-Achse aufgetragenen Verlust wieder auszugleichen. Der zunehmende Abstand der horizontalen Linien verdeutlicht, in welchem Ausmaß sich die notwendigen Prozentgewinne erhöhen müssen, um zunehmende Verluste auszugleichen.
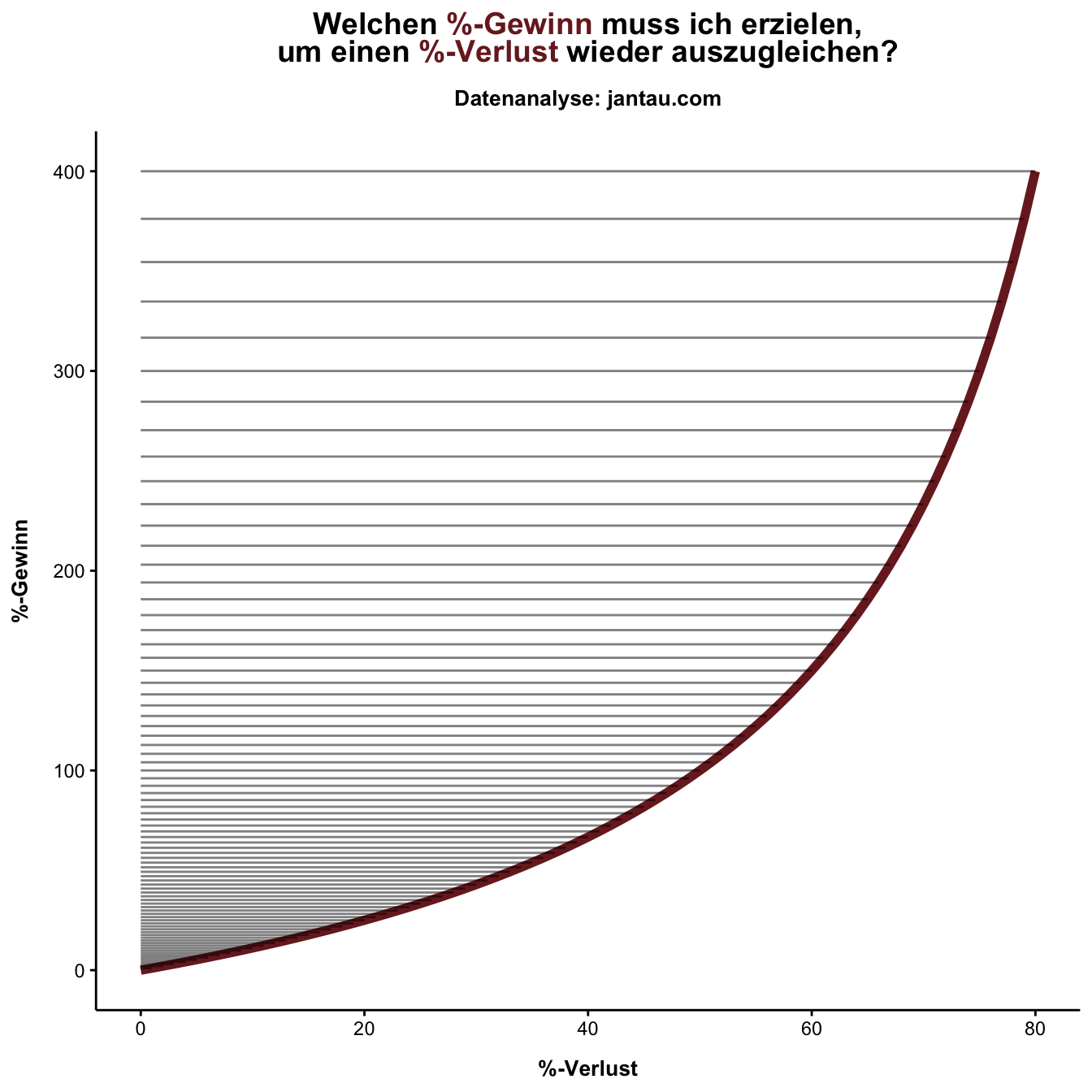
Was bedeutet dieser Effekt für den Anleger?
Für den Anleger bedeutet es, dass er eine Investition lange vorher abschreiben sollte, bevor sie einen 100-prozentigen Totalverlust erleidet. Habe ich 80 % mit einer Aktie verloren – was mit Einzelaktien durchaus passieren kann – dann muss ein erheblicher Turnaround von 400 % erfolgen, um letztendlich einen positiven Ertrag zu erzielen. Sind 400 % auf dem Aktienmarkt möglich, so setzt ein 95 % Verlust einen anschließenden Gewinn von 1900 % voraus, um auf den Ausgangswert zurück zu kommen, was bei einem Titel, der zuvor so extrem eingebrochen ist, ein äußerst unwahrscheinliches Szenario bedeutet.
Die nächste Grafik begrenzt die X-Achse nicht bei 80 %, sondern erst bei 99 %, was die extreme Entwicklung verdeutlicht. Die horizontalen Linien illustrieren den nötigen Gewinn in Prozent, um jeweils 1 % Verlust auszugleichen.
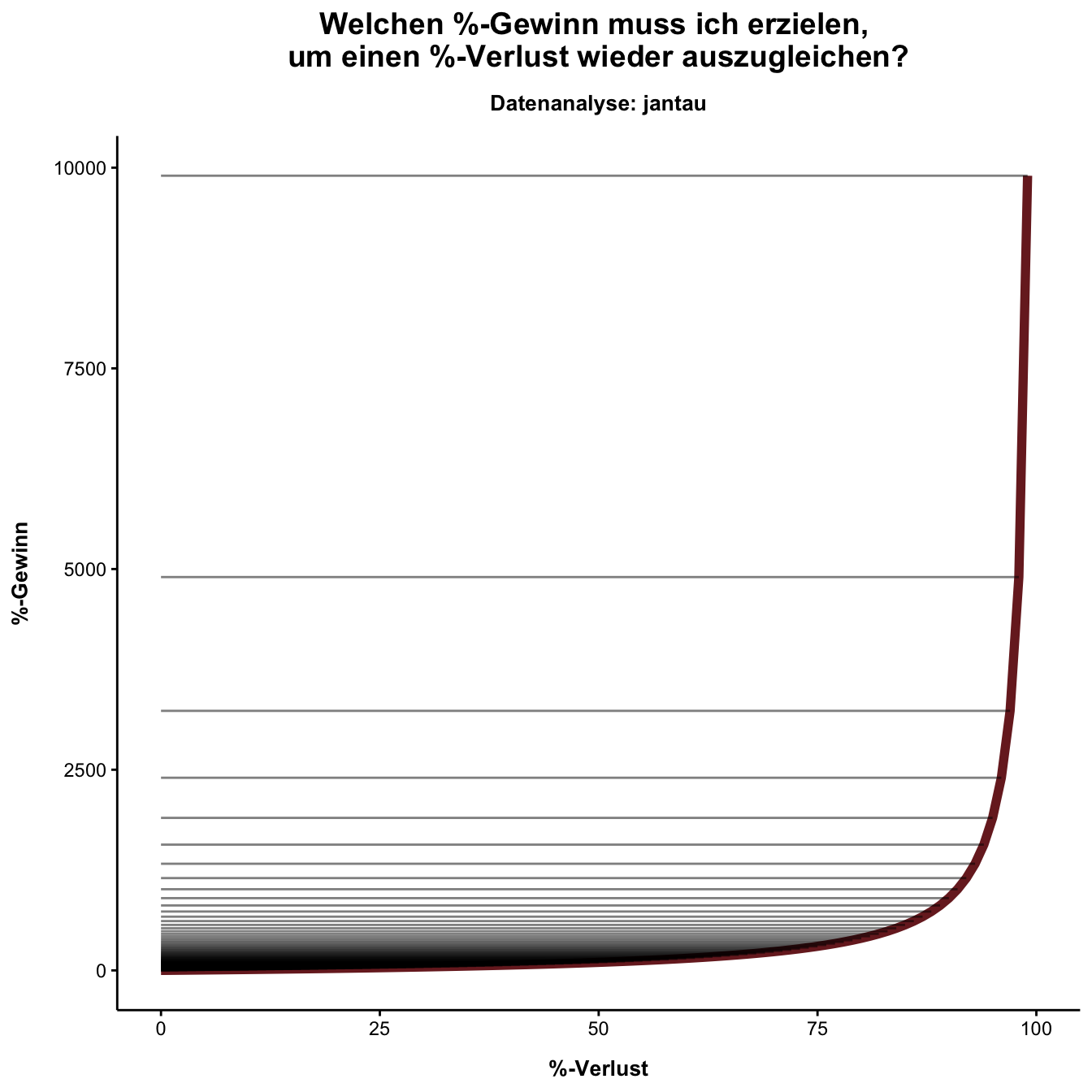
Wirecard als plakatives Beispiel
Der Kursverlauf der Wirecard-Aktie zeigt plakativ den Effekt. Die Aktie hat zum Ende des Jahres 2020 einen Verlust von 99,8 % zum Jahreshöchstwert (143,8 € am 12.2.2020) verzeichnet. Diese extreme Entwicklung kann eine Darstellung des Kursverlaufs nicht mehr abbilden. Nach dem Absturz im Juni 2020 scheint nicht mehr viel zu passieren, da eine Veränderung von beispielsweise 0,2 % bei diesem extremen Kursverlauf nicht mehr groß ins Gewicht fällt.
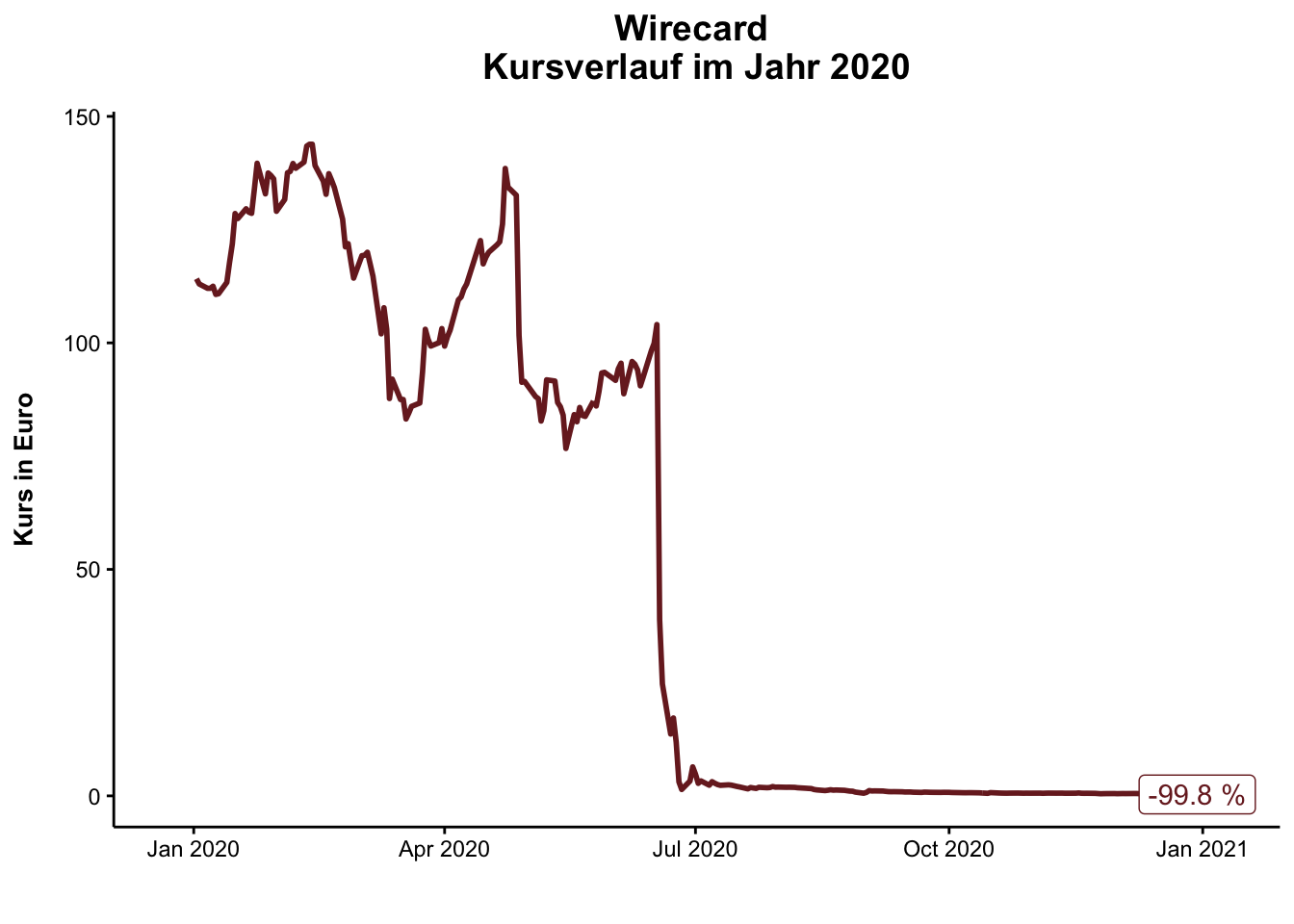
Wird die Darstellung jedoch umgedreht und nicht der Kursverlauf angezeigt, sondern die erforderliche Entwicklung in Prozent, um zum Jahreshöchstwert zu gelangen, so wird die im Plot zuvor nicht ablesbare Entwicklung ab Juni 2020 betont. Die veränderte Darstellung verdeutlicht, welche positive Entwicklung notwendig ist, um zum Jahreshöchstwert 2020 zu gelangen, der mit 143,8 € noch weit vom Allzeithoch entfernt war.
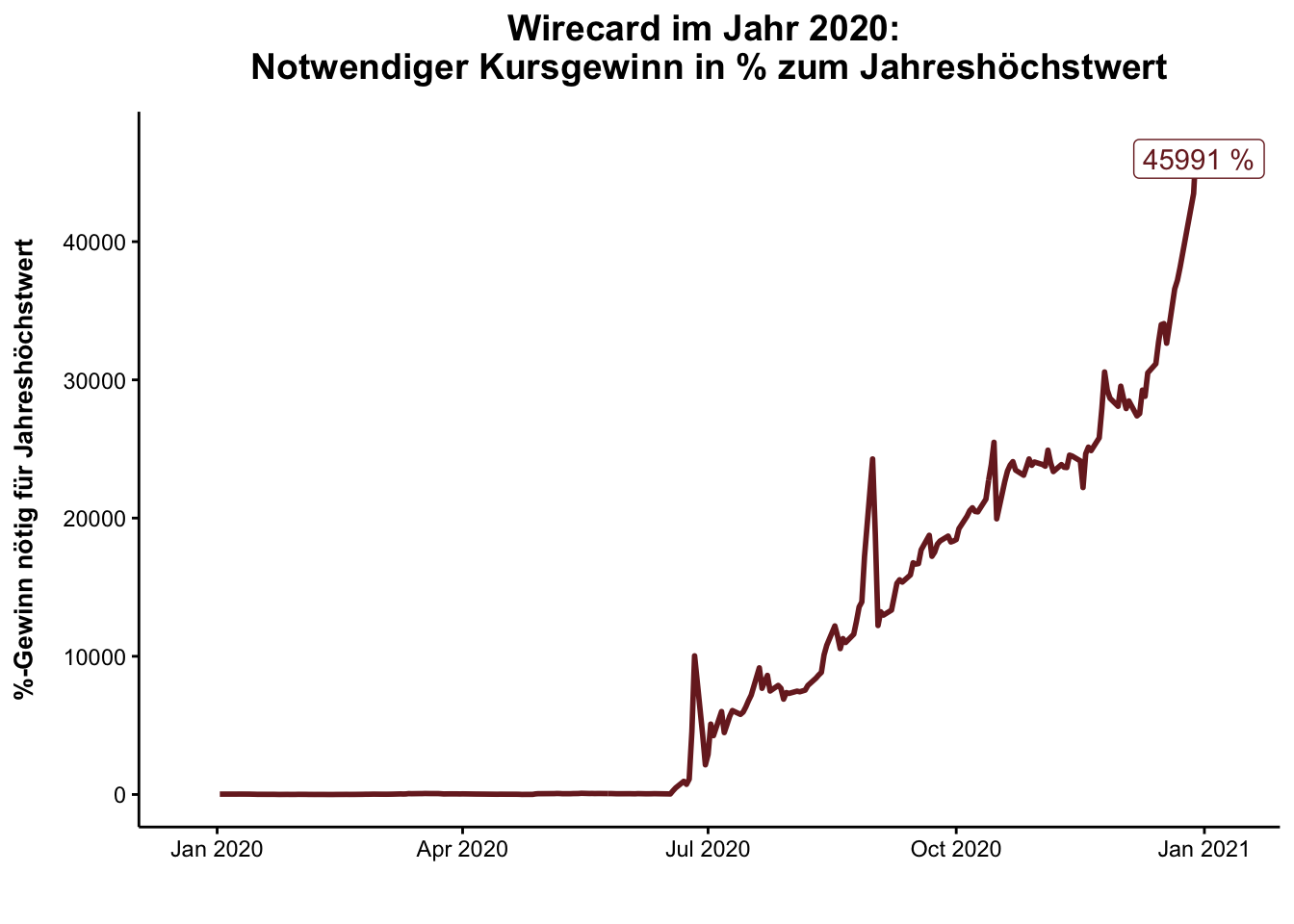
Ein Argument gegen Hebelprodukte
Justin Czyszczewski argumentiert in dem Post Why You Shouldn’t Buy Leveraged ETFs, dass die Rendite durch gehebelte ETFs durch den oben beschriebenen Effekt negativ beeinflusst wird. Gehebelte oder leveraged ETFs bilden den Kursverlauf eines Index nicht eins zu eins nach, sondern hebeln ihn. Ein dreifach gehebelter ETF auf den Dax 30 erzielt die dreifache Kursentwicklung. Steigt der Dax um 1 %, so steigt der gehebelte ETF um 3 %. Fällt der Dax um 2 %, so fällt der ETF um 6 %. Neben höheren Gebühren ist es die hohe Volatilität, die die Rendite schmälert. Fällt der Dax um 1 %, so muss er um 1,010101 % steigen, um zum Ausgangswert zu gelangen. Damit das gehebelte Produkt wieder zum Ausgangswert gelangt, muss der Dax jedoch um 1,030928 % steigen. Ein kleiner Unterschied, der sich jedoch durch die tägliche Berechnung der gehebelten ETFs aufsummiert und mit zunehmender Volatilität weiter steigt.
Den für diesen Beitrag erstellten Code findest du hier: https://github.com/jantau/jantau